Mine did not install ![]()
Have you tried the 2nd version?
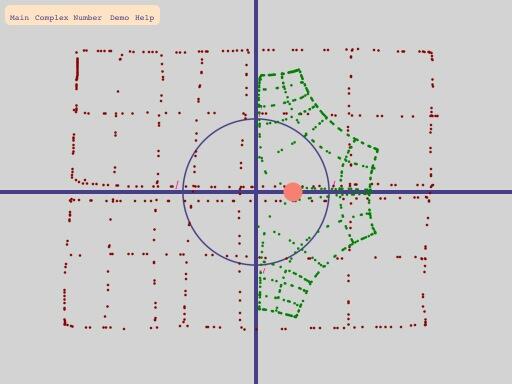
@andrew i see from your app a nice mapping of cicles in the complex plane: circles remain circles when inverted. The infinite space of modulus higher than is mapped onto the finite disc of modulus lower than one. These facts surely have some application in some fields.
Angles are preserved too.
Do you know where this has an application?
I see that the points creation slow down when there are more points. Could you use backened mode so the speed is constant no matter how many points?
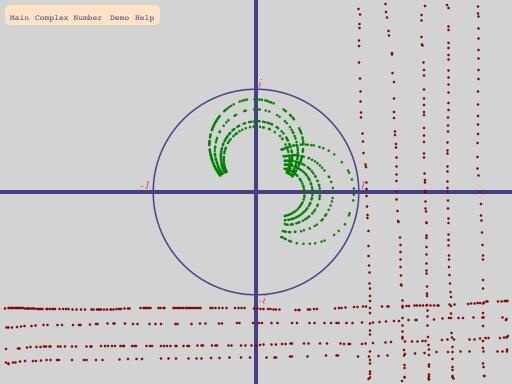 .
.
Hyperbolic geometry or something?
As Mark says, the currently selected operation could be visible
When i select root there is a big dial with 109 that appears in the middle. What is it for? Doesnt react or change to my touch.
The ‘exponential’ operation: what is it doing exactly? Can you show the formula?
109 is the operator number in Mongolia. Maybe that’s where Andrew is working.
Lol! (how can you know the mongolia opperator number???)
Here is some more:
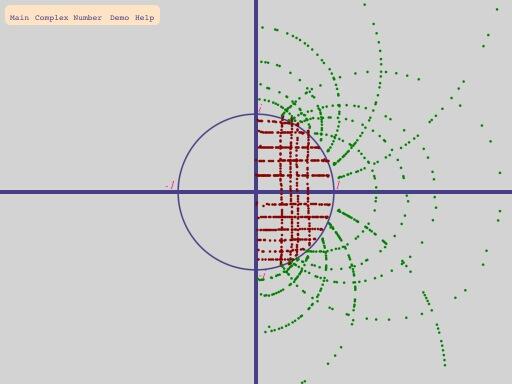 .
.
The inside rectangular grid maps onto a nice series of circles outside, looking pretty much like field lines of capacitor or coil. Any relationship there? Is is property used to solve some physics equation in electromagnetism?
Btw, on the ‘basics’ side, i think a vector representation (as an option) would be more useful to visualize addition and multiplication.
‘clear’ button on direct access: better when freehand drawing (and backened mode, please)
Jmv38 the one called 1.1?
Wow! When you guys test something, you really test it. That’s a slew of great comments and feedback for me to work through.
@West I’ll put a “I’m an engineer get me out of here!” option in to switch i to j (though I’d also have to reflect the plane since, as everyone knows, j = -i.)
@Jmv38 To pick up on just a few of your points. With regard to speed, one problem with a backened mode is that the points can be changed. If you’re doing addition, for example, then as you move the control point then you move all the computed points. I could use noSmooth and noStroke and see if that helps with the speed.
The target audience is people encountering complex numbers for the first time and being presented with just a load of algebraic manipulations to do. The prime example being students that I teach where we give them a couple of lectures on complex numbers before moving on to something else (which then uses them a bit). Learning a load of algebraic manipulations is fine, but doesn’t show the underlying geometry of the complex plane. This is intended to fill that gap. The idea is that they discover the relationships as they explore - much as @Jmv38 has been doing above!
On that, Jmv38, then a transformation that preserves angles is called conformal. On the complex plane then there is a special class of such operations called Möbius transformation. These are ones that take the form z -> (a z + b)/(c z + d) where a,b,c,d are fixed complex numbers. This includes addition (by a fixed number), multiplication (by a fixed number), and reciprocals - but not exponentiation (which is the formula z -> w^z where w is the control point). Both conformal and Möbius transformations are incredibly useful in mathematics. I would guess that they are outside maths as well, but I’m a pure mathematician and now that you know the words then you can read up on Wikipedia as well as I can!
@corneliuhoffman Yes, build 1.0 had some weird bug where it wouldn’t install but build 1.1 installed fine on my iPads.
.@andrew nostroke and nosmooth should surely help! And thanks for the moebius explanation.
@ignatz : both. (lol). No, seriously: i dont know many aspects of complex numbers (like electronics or math transforms) but i work in image processing and i really understand discrete fourier transform (i also teach signal processing in university as a side activity), so i am quite used to complex numbers. And i love to play with visual math tools…
hmmm mine still fails to install… I am starting to think there are issues with my account on testflight
quick question, are you seeing my ipad 1 or mini?
I think that is it, stupid me… I had only my ipad 1 registered… will try tonight
@corneliuhoffman Originally I only had one of your ipads registered (I think the iPad 1). I’ve added the other, but it’ll have to wait until I do a new build.
@Jmv38 Yes, I noticed that too. I’ll fix that in the next build.
When i use the exponontial parameter with a seed on the real axis, it split the half-plane of negative values along the real axis as with a zipper. If i used 1/2 for the seed the plane is transformed into the half plane of positive values. What does that lead to? Isnt there somthing like the zeta rieman function and zeros all located on the x=1/2 axis?